Imagine walking into a massive library in search of a specific book, but without an organized catalog. You’d have to browse through every shelf, which could take hours or even days. However, if the library is equipped with a well-organized catalog, you can simply refer to a systematic list of titles, authors, or subjects, and quickly locate the book you need. This structured approach makes finding the book much faster and more efficient

Similarly, in a database, indexing serves as that organized catalog. It improves query performance (opens new window) by creating a system that allows the database to swiftly locate and retrieve records (opens new window). Just like a catalog helps you find a book quickly, an index helps the database find the data you need much faster. To achieve this, databases use different indexing algorithms (opens new window). For example, hash indexing is effective for exact-match queries (opens new window), quickly finding specific data. Another method, B-Tree indexing, organizes data in a structured way that speeds up searches.

Additionally, graph indexing optimizes searches for data with complex connections, such as relationships in social networks. An index acts as a roadmap in a database, offering quick access to relevant information (opens new window) without scanning every record. This is essential for managing large datasets where both speed and accuracy are critical.

B-Tree Indexing Algorithm

In database management, the B-Tree indexing algorithm is crucial for optimizing search, insert, and delete operations. Its design and properties make it particularly effective for managing large datasets efficiently.

How the B-Tree Index Works

The B-Tree maintains balance by allowing nodes to have multiple children, unlike binary search trees (opens new window), which typically have only two child nodes. This design enables each node to store multiple keys and pointers to its child nodes, ensuring that all leaf nodes remain at the same depth and providing efficient access to data.

These features contribute to the key properties of B-Tree indexing. With its balanced structure, a B-Tree guarantees O(log n) time complexity for search, insertion, and deletion operations. Each node can hold between t-1 and 2t-1 keys and between t and 2t children, offering flexible storage. This balance ensures that the tree’s height remains logarithmic relative to the number of keys, which supports efficient operations even with large datasets. Additionally, the sorted keys within the nodes facilitate efficient range queries and ordered traversals, further enhancing the tree's performance.

Let’s understand it with the help of an example.

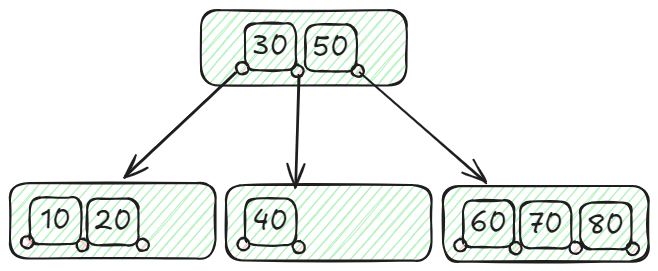
Consider a student database where we need to efficiently search for student records by their IDs. Suppose we have the following student IDs to index: 10, 20, 30, 40, 50, 60, 70, and 80. We construct a B-tree with a minimum degree (t) of 2.

Within this B-tree, the primary node holds two keys (30 and 50), leading to three offspring nodes: the left node preserving IDs below 30 (10, 20), the center node accommodating IDs ranging from 30 to 50 (40), and the right node storing IDs exceeding 50 (60, 70, 80). This organization enables effective handling and retrieval of student IDs using the B-tree data structure. As an example, to locate ID 40, you would begin at the root and observe that 40 falls between 50 and 30. Therefore, you proceed to the middle child node containing 40. This well-balanced organization guarantees efficient search, insert, and delete functions with a time complexity (opens new window) of O(log n).

Advantages of B-Tree Indexing

B-Tree indexing is highly valued for its flexibility and efficiency in managing ordered data. Key advantages include:

1. Efficient Filtered Searches: The ability to quickly narrow down nodes based on specific criteria, combined with the balanced and sorted nature, makes B-Trees particularly effective for filtered searches. This efficiency in handling complex filters helps maintain high performance across large datasets.
2. Consistent Performance: The balanced nature of B-Trees ensures that search, insertion, and deletion operations have predictable performance, typically with a time complexity of O(log n). This balance helps maintain efficiency even as the dataset grows.
3. Efficient Dynamic Updates: B-Trees are well-suited for databases where frequent insertions and deletions (opens new window) occur. Their ability to maintain balance and optimize search paths makes them adaptable to dynamic environments, where the data structure continuously changes.
4. Effective Range Queries: The sorted nature of keys within B-Trees supports efficient range queries and ordered traversals. This capability is particularly useful for operations that require accessing data within specific ranges or sequences.
5. Optimized Disk Usage: B-Trees reduce the number of disk accesses required for search operations by storing multiple keys and pointers per node. This design minimizes disk I/O operations, enhancing performance for large datasets.

Limitations of B-Tree Indexing

Despite its strengths, B-Tree indexing may not always be the best choice in every scenario. Consider the following limitations:

1. Scalability Issues with High-Dimensional Data: As the dimensionality of the vectors increases, the performance of B-Trees can degrade. This makes them less suitable for databases where the majority of data is high-dimensional.
2. Overhead in Static Environments: For datasets that are predominantly static or read-only, the overhead associated with maintaining the balanced structure of a B-Tree may outweigh its performance benefits. In such cases, simpler indexing methods might be more efficient.
3. Complexity and Memory Usage: Implementing and managing a B-Tree can be complex compared to simpler data structures. Additionally, the need to store multiple keys and pointers per node can lead to higher memory usage, which might be a consideration in memory-constrained environments.
4. Higher Memory Usage: The need to store multiple keys and pointers per node in a B-Tree can lead to higher memory usage, which might be a concern in vector databases dealing with large datasets.

Database administrators often choose between B-Trees and hash-based indexing based on their needs. B-Trees excel in relational databases, efficiently managing sorted data and range queries in low-dimensional spaces, and maintaining order for traditional operations.

However, in vector databases that handle high-dimensional data (such as those used in AI and machine learning), B-Trees struggle due to the curse of dimensionality. As dimensions increase, B-Trees become less effective because data spreads more uniformly, making partitioning difficult. In such cases, hash-based indexing offers a compelling alternative, which we will discuss next, and may provide better performance for high-dimensional datasets.

Hash Indexing Algorithm

Hash indexing is a technique designed to enhance search efficiency, especially in high-dimensional contexts like vector databases. It operates differently from B-Trees and is particularly useful for managing large and complex datasets.

How Hash Indexing Works

Hash indexing uses a hash function (opens new window) to map keys to specific locations in a hash table, allowing for efficient data retrieval (opens new window). Unlike B-Trees, which maintain a balanced structure, hash indexes provide constant time complexity, O(1), for search, insertion, and deletion operations, making them ideal for exact match queries. The hash function converts a key into a hash code to determine its index in the hash table, while buckets store entries at each index. Collision handling techniques, such as chaining (linked lists) or open addressing (probing), manage cases where multiple keys hash to the same index.

In vector databases, hash indexing is adapted for high-dimensional data. Multiple hash functions distribute vectors into various hash buckets. During a nearest neighbor search, vectors from relevant buckets are retrieved and compared to the query vector. The method's effectiveness relies on the quality of the hash functions and how well they spread vectors across buckets. Hash indexing enhances search efficiency for exact matches but is less suited for range queries or ordered data retrieval.

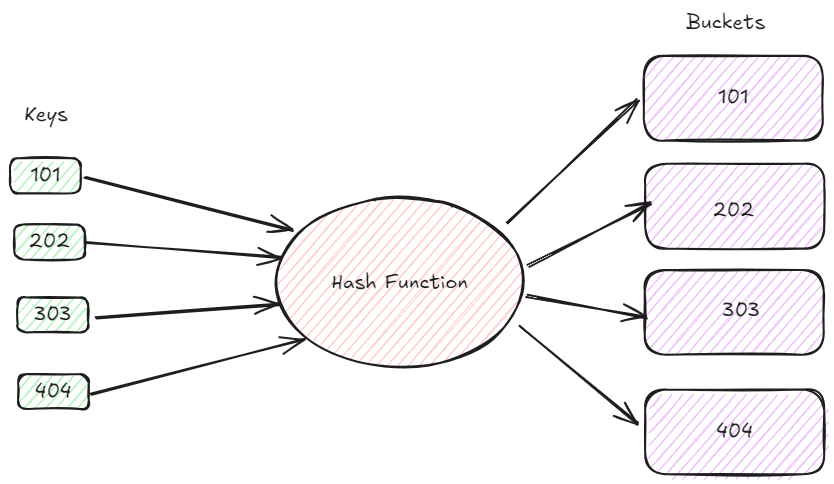
Now to enhance understanding let take a example of a library database where we need to efficiently search for book records by their unique IDs. Suppose we have the following book IDs to index: 101, 202, 303, and 404.

This diagram shows the fundamental idea of hash indexing. We begin with a collection of book IDs, which serve as our keys. The keys go through a hash function that changes them into numerical values. These hash values, labeled as such, decide the container where the related book data will be placed. Ideally, the hash function evenly distributes the keys among the buckets to reduce collisions. In this instance, every book ID is linked to a distinct bucket, showcasing flawless hash distribution. In actual situations, collisions are frequent and need additional methods such as chaining or open addressing to manage them successfully.

Advantages of Hash Indexing

1. Fast Lookup: Hash indexing provides average-case constant time complexity O(1) for search operations, making it extremely efficient for exact match queries.
2. Simple Structure: The hash table structure is straightforward, which simplifies implementation and management compared to more complex structures like B-Trees.
3. Efficient for Point Queries: Hash indexing excels in scenarios where queries are based on exact matches, such as retrieving a record by a unique identifier.

Limitations of Hash Indexing

1. Inefficient for Range Queries: Hash indexing is not well-suited for range queries or ordered data access because the hash function does not preserve the order of keys.
2. Collision Handling Overhead: Handling collisions can add overhead, particularly if the hash table is not well-sized or if collisions are frequent.
3. Fixed Size Table: Hash tables often have a fixed size, and resizing them can be complex and costly. This might lead to performance degradation if the table becomes overloaded.
4. Lack of Flexibility: Unlike B-Trees, hash indexes do not support efficient range queries or ordered traversals, which can be a significant drawback for applications that require such operations.

While hash indexing is great for fast exact match queries, it can struggle with high-dimensional data. For efficient approximate nearest neighbor (ANN) searches, graph indexing using the HNSW (Hierarchical Navigable Small World) algorithm provides a powerful alternative, adeptly managing complex, high-dimensional vectors.

Boost Your AI App Efficiency now

Sign up for free to benefit from 150+ QPS with 5,000,000 vectors

Free Trial

Explore our product

Graph Indexing

Graph indexing (opens new window) is very useful for handling complex data networks or relationships, like social connections or recommendation systems. Graph indexing, in contrast to linear data structures such as B-Trees or hash tables, is specifically designed to effectively handle and retrieve graph data, where the connections between entities hold equal significance to the entities themselves.

In modern vector databases, graph-based indexing (opens new window) methods like HNSW (Hierarchical Navigable Small World) (opens new window) are widely used for approximate nearest neighbor (ANN) (opens new window) searches, especially in high-dimensional spaces. These advanced techniques are designed to navigate through large and complex datasets efficiently.

How Graph Indexing Works

Graph indexing involves creating structures that help quickly locate nodes (vertices) and edges (connections) based on specific queries. The indexing process might focus on different aspects of the graph, such as node labels, edge types, or the shortest paths between nodes. Several graph indexing methods have been developed to optimize different types of queries:

1. Path Indexing: This method indexes specific paths within the graph, making it faster to retrieve common patterns or paths between nodes. It’s particularly useful for queries that involve traversing the graph to find relationships or connections.
2. Subgraph Indexing: In this approach, frequent subgraphs (smaller components of the overall graph) are indexed, allowing for efficient searches when looking for specific patterns or structures within a larger graph.
3. Neighborhood Indexing: This method focuses on indexing the immediate neighbors of each node, which is useful for queries that need to explore connections or relationships directly linked to a specific node.

HNSW (Hierarchical Navigable Small World)

HNSW is an algorithm based on graphs that is specifically created to efficiently find nearest neighbors in high-dimensional vector spaces. The main concept of HNSW involves building multiple hierarchical layers, with each layer being a graph that links nodes (data points) based on their closeness. The upper layers give a general summary, whereas the lower layers present more intricate information.

In practice, when you perform a search using HNSW, the algorithm starts at the top layer and navigates through the graph, gradually descending to lower layers where the search becomes more precise. This hierarchical approach significantly reduces the search space, making it possible to retrieve nearest neighbors quickly, even in very large datasets.

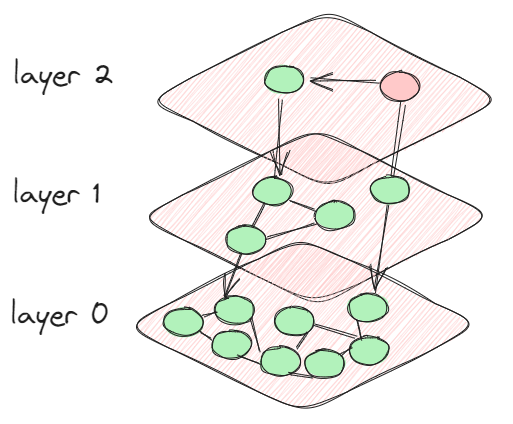
Imagine you're searching for similar images in a large database of visual data. Each image is represented by a high-dimensional vector (e.g., extracted features from a neural network). HNSW allows you to quickly find images that are closest to a given query image by traversing the hierarchical graph, starting from a broad search in the upper layers and gradually zooming in on the closest matches in the lower layers. Graph indexing algorithms like HNSW are designed to minimize the computational cost associated with such traversals, especially in large graphs where millions of nodes and edges may exist. The indexing process significantly improves query performance by focusing on relevant parts of the graph.

Advantages of Graph Indexing with HNSW

1. Optimized for Complex Relationships: Graph indexing excels at managing and querying data with complex relationships, such as social networks, where connections between entities are crucial.
2. Efficient Traversal for ANN Searches: HNSW is highly efficient in performing approximate nearest-neighbor searches, which are crucial for tasks like image retrieval, recommendation systems, and other applications involving high-dimensional data.
3. Scalability: HNSW scales well with large datasets, handling millions of vectors with relatively low latency.
4. Flexibility: HNSW can be adapted for various use cases and offers a balance between search accuracy and computational efficiency.

Limitations of Graph Indexing with HNSW

1. Approximate Results: HNSW is designed for approximate nearest neighbor searches, meaning it may not always return the exact closest match, though it typically offers a good trade-off between speed and accuracy.
2. Complex Implementation: Graph indexing, including HNSW, is more complex to implement compared to traditional indexing methods like B-Trees or hash indexing. It requires specialized algorithms tailored to specific types of queries and graph structures.
3. Resource-Intensive: Due to the complexity of graph data, indexing, and querying can be resource-intensive, requiring more memory and processing power.
4. Memory Usage: The multi-layered graph structure of HNSW can consume a significant amount of memory, which might be a consideration in resource-constrained environments.

While B-Trees and hash indexing work well for certain types of queries, they struggle with complex or high-dimensional data. Graph indexing methods like HNSW handle these challenges by efficiently navigating complex connections. The Multi-Scale Tree Graph (MSTG) from MyScale (opens new window) takes this a step further by combining the best of SQL and graph-based techniques. MSTG uses a mix of hierarchical tree structures and graph traversal to quickly and accurately search through large, complex datasets. This blend makes it a powerful tool for handling today’s vast and intricate data.

Multi-Scale Tree Graph (MSTG)

The Multi-Scale Tree Graph (MSTG) algorithm, developed by MyScale (opens new window), is an advanced indexing technique designed to overcome the limitations of traditional vector search algorithms like HNSW (Hierarchical Navigable Small World) (opens new window) and IVF (Inverted File Indexing) (opens new window). MSTG is particularly well-suited for handling large-scale, high-dimensional vector data, offering superior performance for both standard and filtered searches.

How MSTG Works

MSTG combines the strengths of hierarchical tree clustering and graph traversal to create a robust and efficient search mechanism. Here’s how it works:

1. Hierarchical Tree Clustering: At the initial stage, MSTG uses a tree-based clustering approach to organize the data into clusters. This hierarchical structure helps in reducing the search space, making the retrieval process faster and more efficient.
2. Graph Traversal: (opens new window) Once the data is organized into clusters, MSTG applies graph traversal techniques to navigate between these clusters. This enables quick and accurate retrieval of the nearest neighbors, even in complex, high-dimensional spaces.
3. Hybrid Approach: The hybrid nature of MSTG allows it to efficiently manage both dense and sparse regions of the vector space. This adaptability is key to its performance, especially in large datasets where traditional algorithms might struggle.

Overcoming the Limitations of Other Algorithms

MSTG addresses several key limitations of existing vector search algorithms:

1. HNSW Limitations: While HNSW is effective for unfiltered searches, its performance drops significantly for filtered searches, especially when the filter ratio is low. MSTG overcomes this by maintaining high accuracy and speed even under restrictive filter conditions, thanks to its combined tree and graph-based approach.
2. IVF Limitations: IVF and its variants can suffer from increased index size and reduced efficiency as datasets grow larger. MSTG mitigates these issues by reducing resource consumption and maintaining fast search times, even with massive datasets.
3. Resource Efficiency: MSTG leverages memory-efficient storage solutions, such as NVMe SSDs, to reduce the resource consumption that typically plagues IVF and HNSW, making it both cost-effective and scalable for large-scale applications.

MyScale (opens new window) optimizes the filter vector search (opens new window) with the unique MSTG algorithm that provides a significant leap in performance for vector search tasks, particularly in scenarios involving large and complex datasets. Its hybrid approach and resource-efficient design make it a powerful tool for modern vector databases, ensuring fast, accurate, and scalable search capabilities.

Join Our Newsletter

Subscribe

Making the Right Choice for Your Database

The selection of an indexing algorithm should be tailored to your specific requirements, taking into account the data type, query frequency, and performance needs of your database. For instance, if your database frequently performs range queries or necessitates efficient sorting capabilities, a B-Tree index might be more appropriate due to its optimized structure for such operations. On the other hand, if your primary focus is on exact-match queries and rapid lookups, a Hash index could offer superior performance in those scenarios.

In summary, understanding the distinctive characteristics of each indexing algorithm is essential in making an informed decision that optimizes query performance based on your database's unique requirements.